本文共 6193 字,大约阅读时间需要 20 分钟。
本节书摘来华章计算机《SQL与关系数据库理论——如何编写健壮的SQL代码》一书中的第1章 ,第1.4节 C. J. Date 著 单世民 何英昊 许侃 译 更多章节内容可以访问云栖社区“华章计算机”公众号查看。
1.4 原始模型回顾
此节可以充当后续讨论的起点;本节回顾原始定义的关系模型中一些最基本的方面。请注意限定词“原始定义”!关于关系模型的一个广为传播的错误观念就是,它完全是静态不变的。事实并非如此。在这方面,关系模型很像数学:数学也不是静态的,可随时间不断发展。事实上,关系模型本身可以被视为是数学的一个小分支;同样,它也随着新证明的定理和新发现的结果而不断演进。而且,任何有能力的人都可以做出这些贡献;正像数学的其他分支一样,尽管最初是由一个人发明的,关系模型现在已经成为了属于全世界的团体成就。
另外,可能你并不知道,关系模型的发明者是E. F. Codd,当时是IBM的研究人员(E表示Edgar,F表示Frank——但是他总是使用首字母来签名;他给他的朋友签名是Ted,作为他的朋友,我非常荣幸)。那是在1968年末,作为一个接受过系统训练的数学家,Codd第一个意识到可利用数学学科为一个领先于时代的远未完善的领域(数据库管理)注入一些坚实的原理与精确性。他对于关系模型的原始定义出现在1969年的一份IBM研究报告中,我会在附录G中对其稍加说明。1.4.1 结构特征
原始的关系模型有3个主要组件——结构(structure)、完整性(integrity)和操作(manipulation)——我会逐一进行简述。不过请注意,我在此处给出所有“定义”是很不严谨的;我会在后续章节中的合适时机让定义更为精确。
首先是结构。当然,主要的结构特征是关系(relation)本身,并且所有人都知道关系通常都在纸面上画成表格形式(参见图1.1,不言自明)。关系定义在类型(type,也被称为域(domain))的基础上,类型是概念上的取值池,实际关系中的实际属性从此池中获取实际的值。以图1.1中所示的简单departments-and-employees数据库为例,应该存在名为DNO(部门编号)的类型以保存所有合法部门编号的集合。这样,DEPT关系中的DNO属性和EMP关系中的DNO属性就都可以包含来源于此概念池的取值了。(顺便提一下,尽管让属性和对应的类型使用相同的名称是个好主意,但是这样做是没有必要的,而且它们也经常不相同。我们稍后会看到大量的反例。)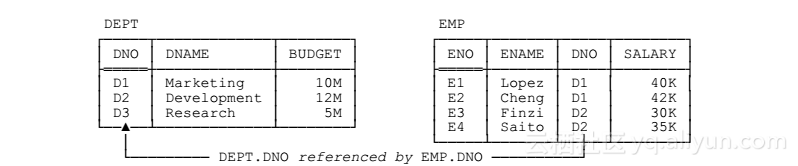
图1.1:departments-and-employees数据库——样例值
正像我所说的,图1.1中的表格描述了关系,准确地说就是描述了n元关系(n ary relations)。n元关系可被描述为有n个列的表;其中,列代表关系中的属性,行代表元组。n的值可以是任何非负整数。n等于1称为一元(unary)关系, n等于2称为二元(binary)关系,n等于3称为三元(ternary)关系,依次类推。关系模型还支持很多种键(key)。首先(此点很关键),每个关系都至少有一个候选键(candidate key)注4。候选键就是唯一标识符;换句话说,它是属性的组合——经常是只有一个单一属性的“组合”,但也未必总是——使得关系中的每个元组对于这样的属性组合都有唯一的值。比如,在图1.1中每个部门都有一个唯一的部门编号,每一个员工也都有唯一的员工编号,所以我们可以说{DNO}是DEPT表的候选键,而{ENO}是EMP表的候选键。要注意大括号,(哪怕只包含一个属性)候选键也是属性的组合(或者说是集合),而文献中集合的惯用表示方式就是封闭在大括号中的元素列表。旁注:这是我首次提到“列表”(commalist)这个有用的词,而我会在后续内容中大量使用它。“列表”可以如下定义:令xyz为某语法结构(比如“属性名称”),则“xyz列表”表示0个或多个xyz的序列,并且序列中所有相邻的xyz配对之间都用逗号分隔(在逗号的前后可以有一个或多个空格)。比如,如果A、B和C是属性名称,那么如下所示的就都是属性名称列表:A , B , C C , A , B B, A , C
对于不包含属性名的空序列也是一样。
另外,如果列表在大括号中,并因此表示集合,则有:(a)列表中元素出现的顺序是不重要的(因为集合不对元素进行排序),(b)如果元素出现多次,则该元素等同于出现一次(因为集合不包含重复元素)。其次,主键(primary key)是被挑出来特殊对待的候选键。如果某个关系只有一个候选键,那么我们就不必把这个候选键称为“主要的”。但是如果关系有两个以上的候选键,那么通常选择其中一个作为“主要的”,这意味着它多少“比其他属性要高一等”。比方说,假设每个员工总有唯一的员工编号和唯一的员工姓名(这个例子可能不很实际,不过对于当前目标足够了),则{ENO}和{ENAME}都是EMP的候选键。此时,我们可以选择{ENO}作为主键。要注意,我说的是“通常”会选择一个主键。选择主键确实是通常要做的,但不是一定必须做的。如果只有一个候选键,那么没选主键也没问题;但是,如果有两个以上的候选键,而又不得不选择其中一个作为主键,那么不管选哪个都多少有点主观意味(起码对我是如此)。肯定会存在我们找不到什么好理由作为选择依据的情况。因此,我在本书中通常遵循主键准则——在类似图1.1的图中,我会使用双下划线标示主键注5——不过要强调的是,从关系化视角来看,重要的是候选键而不是主键。因此,我以后会用未加限定的术语“键”来表示任何候选键,不管它是否为“主要的”。(请注意,主键凌驾于其他候选键之上享受的“特殊对待”本质上来说主要是在语法上的,它既不是根本性的也不是很重要的“特殊对待”。)最后,“外键”是某关系r2中的一个属性组合(或集合)FK,且要求FK的每个取值都与另一关系r1中某个键K的某个取值相等(r1和r2不必是不同的关系)注6。以图1.1为例,{DNO}是EMP中的外键,其值要求匹配DEPT中键{DNO}的取值(如图1.1中用适当标记的箭头所暗示的那样)。此处的“要求匹配”指的是,如果EMP包含了一个DNO属性取值为D2的元组,则DEPT中必须也包含DNO值为D2的元组;否则EMP就会出现身处根本不存在部门的员工,数据库也就不再是“现实的真实模型”(a faithful model of reality)了。1.4.2 完整性特征
完整性约束(integrity constraint,简称为约束)基本上就是结果必须为TRUE的布尔表达式。以部门和员工为例,我们可以用一个约束,即SALARY值必须大于0。任何确定的数据库都要服从大量约束;然而,所有这些约束又都必须特定于所属数据库,并由数据库中的关系来表达。相反,最初表述的关系模型包括两个“通用(generic)”的约束——可以说,通用指的是它们适用于所有数据库。这两个通用约束一个与主键有关,另外一个和外键有关。如下:
- 实体完整性规则(The entity integrity rule):主键属性不允许null。
- 参照完整性规则(The referential integrity rule):不能存在任何不匹配的外键取值。
先解释第二个规则。术语“不匹配的外键取值”指的是相关候选键(即“目标键”)中没有与外键取值相等的取值;比如,如果departments-and-employees数据库中包括一个DNO值为D2的EMP元组,但不包括具有同样DNO取值的DEPT元组,那么它就违反了参照完整性规则。所以,参照完整性规则直接表明了外键的语义;名称“参照完整性”源于如下事实:外键取值可认为是对于所对应目标键具有相同取值的元组的“参照”。因此,此规则实际上是说:如果B参照A,则A必须存在。
至于实体完整性规则,有一个问题。事实上,我完全反对null的概念;也就是说,我强烈认为“null在关系模型中没有位置”。(很明显,Codd的想法正好相反,可我能拿出强有力的理由来支持我的立场)。因此,为了解释实体完整性规则,我要搁置怀疑,先假设它是成立的我会在第3章和第4章中重提null的整个议题。本质上,null是表示“值未知”(value unknown)的“记号”(mark)。重要的是,它本身不是值;再说一遍,它是一个记号,或标记(flag)。比方说,假设我们不知道员工E2的工资,那么我们就不能为EMP关系中对应于员工E2的元组输入某个实际的SALARY值(根据定义,我们不能输入实际值,因为我们不知道该值到底应该是什么),我们应该将其元组的SALARY位置标记为null,如下所示: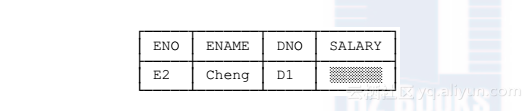
重要的是,要理解这个元组在SALARY位置根本什么都没包含。但把根本什么都没有图示出来太难了!我尝试在上图中使用阴影来说明SALARY位置是空的,但是连那个位置都不显示应该是更准确的。虽然如此,我还是在本书其他地方用同样的阴影方式来代表空位置,不过要记住,所用的阴影并不代表任何种类的值。如果你喜欢,你可以把它(即阴影)想成null的“记号”(或标记)。
回到实体完整性规则:对于EMP关系,通常来说,该规则说明确定的员工元组可以有未知姓名,或者未知部门编号,又或者是未知工资,但是不可以有未知员工编号。理由是:如果员工编号未知,那么我们甚至不知道我们正在谈论哪个“实体”(entity)(即员工)。关于null现在就说这么多。在下次提到之前把这些内容忘了吧。1.4.3 操作特征
关系模型的操作分为两部分:
- 关系代数,即可用于关系的运算符的集合(比如,差或MINUS)。
- 关系赋值运算符,此运算符允许将关系表达式(比如,r1 MINUS r2,其中r1和r2为关系)的值赋给关系。
关系赋值运算符是关系模型实现更新的基础方式,后续的1.8节“关系vs.关系变量”会详细说明。注意,本书按照惯例使用通用的术语“更新”(update)来在总体上指代INSERT、DELETE和UPDATE(及赋值)运算符。当我要特指UPDATE运算符时,我会像刚才一样将其全部大写。
至于说关系代数,可以很不严谨地说,它由一套允许我们从“旧”关系中导出“新”关系的运算符组成。每个这样的运算符都是用一个或多个关系作为输入,并产生另一个关系作为输出。比如,差(MINUS)使用两个关系作为输入,并从一个中“减去”另外一个,以此产生一个作为输出的关系。非常重要的是,输出是另一个关系:这也正是关系代数有名的闭包(closure)性质。正是闭包性质使我们能写出嵌套的关系表达式,因为任何运算的输出都和输入属于同一类型,一个运算的输出可以成为另一个运算的输入。比如,我们可以进行差运算r1 MINUS r2,将其结果和关系r3一起作为并运算的输入,然后再将新的运算结果和关系r4一起作为交运算的输入,依此类推。任意多个运算符都符合“输入一个或多个关系,只输出一个关系”的简单定义。此处要简述通常所认为的原始运算符(其实就是Codd在他最早的论文中定义的那些)注7;第6章会给出更多细节,而第7章会讲解一些附加运算符。图1.2是原始运算符的图示。注意:如果你不熟悉这些运算符,觉得此处的讲解有点难于理解,那也不用担心。我说过,后面的章节中会用大量示例来详细地讲解。限制(restrict)返回一个关系,其中包含特定关系中满足特定条件的所有元组。比如,我们可以限制EMP关系得到DNO值为D2的那些元组。投影(project)返回一个关系,其中包含特定关系移除特定属性后的所有(子)元组。比如,我们可以只对EMP关系中的ENO和SALARY属性进行投影(也就是去除ENAME和DNO属性)。积(product)返回一个关系,其中包含所有的可能由两个元组组合形成的元组,进行组合的两个元组分别来自于两个指定的关系。注意:这个运算符也称为笛卡尔积(有时也叫扩充的或扩展的笛卡尔积)、交叉积,交叉连接或笛卡尔连接;事实上,在第6章中我们会知道它只是连接(join)的特例。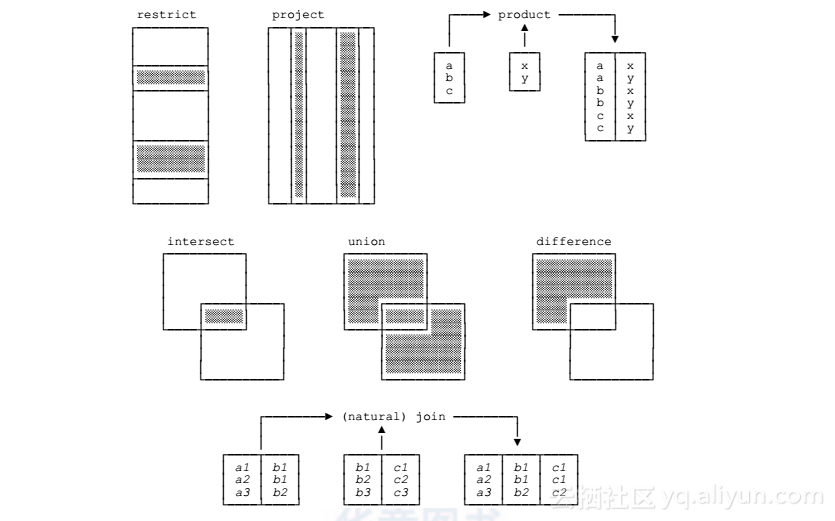
图1.2:原始的关系代数
交(intersect)返回一个关系,其中包含同时在两个指定关系中都出现的所有元组。(像积一样,在第6章我们会知道“交”实际上也是连接的特例。)并(union)返回一个关系,其中包含在两个指定关系中出现过的所有元组。差(difference)返回一个关系,其中包含在第一个指定关系中出现但在第二个指定关系中没有出现的所有元组。连接(join)返回一个关系,其中包含的元组是由分别来自于两个指定关系的元组组合而成的,并且进行组合的元组之间在两个关系的同名属性上具有相同的取值(而且,在结果元组中,相同取值只出现一次而非两次)。注意:此种连接原来称为自然连接,以便与本书后续内容所讨论的其他各种连接相区别。不过,因为自然连接是最重要的连接类型,所以用未加限定的术语“连接”来特指“自然连接”已经成为了行规,本书会遵守此行规。本节最后一点:你或许知道存在所谓的关系演算(relational calculus)。关系演算可认为是关系代数的替代品;也就是说,我们既可以说关系模型的操作部分是由关系代数(加上关系赋值)构成的,也同样可以说它是由关系演算(加上关系赋值)构成的。每个关系代数表达式都存在逻辑等价的关系演算表达式,反之亦然。从这个意义上说,两者是等价且可互换的。我们将在第10章和第11章详细介绍关系演算。1.4.4 运行示例
最后,我要介绍一下本书绝大多数讨论所依据的示例:大家都很熟悉的(近乎陈腐的)suppliers-and-parts数据库(很抱歉,我又把这匹老战马拉出来了。不过,我相信使用这个在大量出版物中都用过的示例会有利于读者学习。)样例取值如图1.3所示。
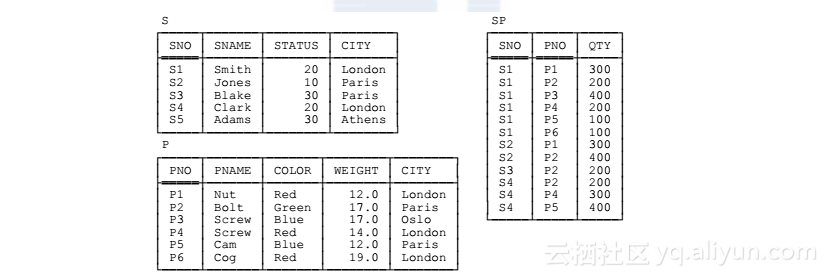
图1.3:suppliers-and-parts数据库,样例数据
供应商(suppliers)关系S表示供应商(准确说,是签订了合同的供应商)。每个供应商有一个唯一的供应商编号(SNO),如图所示,我把{SNO}作为主键。每个供应商还有一个姓名(SNAME),不必唯一(尽管图1.3中的SNAME值看起来恰好唯一);一个状态值(STATUS),表示可用供应商的某种排序或偏好等级;一个地点(CITY)。零件(parts)关系P表示零件(更准确说,是零件种类)。每一种零件有一个唯一的零件编号(PNO)({PNO}是主键);一个名称(PNAME);一个颜色(COLOR);一个重量(WEIGHT);一个存储此种零件的地点(CITY)。出货(shipments)关系SP表示出货(显示了哪些供应商供应了或运送了哪些零件)。每一个出货都有一个供应商编号(SNO),一个零件编号(PNO)和一个数量(QTY)。对于与这个例子,我假设某个供应商对于某种零件在任意时刻至多有一个出货({SNO,PNO}是主键;同时,{SNO}和{PNO}也都是外键,分别对应于S和P的主键)。注意图1.3中的数据包括一个没有任何出货的供应商(S5)。转载地址:http://tgwxa.baihongyu.com/